Eenheidsvectornotatie | Vectoren en spaties | Lineaire algebra | Khan Academy
Wanneer ze dimensie W uitleggen, wordt deze weergegeven als de negatieve kant van de X-as. Waarom is dimensie W negatief X? Is het niet echt zijn eigen dimensie?

- Probeer een 4-dimensionale grafiek te tekenen op een 2-dimensionaal oppervlak. Dit is wat ze bedachten (je hebt gelijk, hoewel het geen geweldige grafiek is).
Zoals @NendoTaka heeft gezegd, is het vrij moeilijk om een 4d-object op een 2D-oppervlak te tekenen.
Dit is hoe dimensionaliteit werkt:
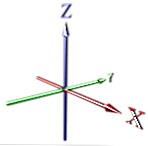
met een enkele dimensie wordt een punt oneindig uitgezonden, waardoor een lijn ontstaat (zie X)
in 2d voegen we een dimensie loodrecht daarop toe (zie X, Y).
Dan gaan we weer loodrecht en breiden uit naar boven om de derde dimensie te krijgen (zie X, Y, Z).
Omdat 3d> 2d, kunnen we dat niet zo goed weergeven op papier zonder het papier te vouwen of er meer vellen bovenop te leggen - allemaal echt onpraktisch om op een scherm te bekijken. Dus in plaats daarvan gebruiken we perspectief - hoe onze ogen 3d waarnemen. Meestal zijn de hoeken hier ~ 30 graden.

En dat ziet er best goed uit, want onze ogen zien niet in deze traditionele 3D-zin, dus nabootsen werkt. Maar als we een 4e dimensie willen vertegenwoordigen, hebben we niets om dat mee te vergelijken. We moeten weer loodrecht gaan staan en dit is moeilijk voor onze ogen te bevatten, omdat we niet echt een referentie hebben.
Hier is een voorbeeldafbeelding van een 4e dimensie:
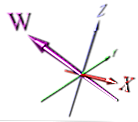
Dit is een correctere manier om de dimensie weer te geven, maar het is nog steeds afhankelijk van perspectief - het is ook niet meteen duidelijk dat het op het eerste gezicht een nieuwe dimensie is.
De animators kozen er waarschijnlijk voor om iets eenvoudigs te doen dat gemakkelijker te animeren zou zijn. Hoewel, als u de bovenstaande afbeelding roteert, de X- en W-afmetingen kunnen overlappen - en dit zou niet duidelijk zijn in de afbeelding zonder pijlwijzers.
Dus ja, ze hebben het mis - maar er is ook geen eenvoudige manier om vier dimensies op één vel papier weer te geven
Coördineer beeldbronnen en lees goed
3- 1 Om eerlijk te zijn, er zijn veel standaardmanieren om 4-dimensionale objecten zoals tesseracten en 3-bollen in 3 dimensies te projecteren (en vervolgens op de gebruikelijke manieren tot 2 dimensies) die veel beter zijn dan degene die in de show wordt gebruikt. waarvan de toegevoegde bonus dat ze er cooler uitzien dan degene die in de show wordt gebruikt.
- @senshin oh zeker, maar ik denk dat de animators ook iets wilden uitleggen, in plaats van verbaasd te zijn
- 1 Je zou andere dingen dan positie kunnen gebruiken om aan te geven hoe ver iets langs een as is, zoals kleur.