Hoe is Misaka's railgun zo destructief?

[Unboxing - BBB] 베이 블레이드 버스트 超王 (슈퍼 킹) 리뷰 3 - B-161 [부스터] 글라이드 라그나 뢰크 .Wh.R 1S 리뷰 & 테스트

In aflevering 1 van Railgun maakt Misaka's railgun een einde aan een flink deel van wat een olympisch zwembad lijkt te zijn. Later in dezelfde aflevering wordt onthuld dat haar railgun reist met een snelheid van 1030 m / s.

De cijfers kloppen echter niet.

Stel dat Misaka munten van 10 gram gebruikt. Bij 1030 m / s, die munt heeft zoveel energie:

Energy = 1/2 m v^2 = 1/2 (0.01 kg) (1030 m/s)^2 = 5304.5 kg (m/s)^2 = 5304.5 Joules

Een olympisch zwembad heeft 2.500.000 kg water. Op basis van de bovenstaande afbeelding reist die kegel waarschijnlijk ruim 100 meter de lucht in.

Dus laten we voor de twijfel zeggen dat slechts 10% van het water 100 meter de lucht in wordt getild.

Energy = m g h = (0.01 * 2500000 kg) (9.8 m/s^2) (100 m) = 2.45 * 10^8 kg (m/s)^2 = 2.45 * 10^8 Joules

De munt heeft 2.45 * 10^8 Joules energie om het zwembad te verheffen, zoals hierboven weergegeven. Maar haar munt kan alleen maar zorgen 5304.5 Joules. Er is een verschil van ongeveer 4 ordes van grootte.

Oké ... Voordat iemand dit afdoet als gewoon een ander geval van Anime-fysica, laten we eens kijken naar wat nog meer zoveel energie zou kunnen produceren:

De spin van de munt wordt niet meegenomen in de netto snelheid van 1030 m / s. Maar gezien het traagheidsmoment van een kleine munt, zou het een enorme (relativistische?) Hoeveelheid spin nodig hebben om te dragen 10^8 Joules.
De lading van de munt is niet gespecificeerd in de Anime. Misschien polariseert Misaka op de een of andere manier de lading in de munt en laat het op de een of andere manier los bij contact met het doelwit.
De massa-energie (E = mc^2) van de munt is 9 * 10^14 Joules. Is dit wat ze deed?

Dus de vraag is: is er een officiële verklaring voor waar de munt zoveel energie krijgt? Of moeten we dit afdoen als een ander geval van Anime-fysica?

En als iemand geïnteresseerd is in de chatdiscussie over de fysica hier: chat.stackexchange.com/transcript/message/7951592#7951592
FWIW, Funimation schreef vorig jaar een blogpost, A Certain Scientific Explanation of Railguns. Helaas lijkt de gekoppelde pdf met de cijfers en de lampekap van hoe verkeerd het is, verloren te zijn gegaan. IIRC, de antwoorden hier dekken al alles wat het zei.
@Mystical door Official bedoel je een puur natuurkundige uitleg of een canonieke uitleg?
@Mindwin Met "Officieel" bedoel ik als de studio of een van de auteurs iets heeft gezegd.

Volgens de anime en manga heeft Mikoto een "mondingssnelheid" van 1030 m / s:

Het railgun van de Amerikaanse marine daarentegen heeft een mondingssnelheid van 2520 m / s (~ 5600 mph of ~ 7,5x de geluidssnelheid), met een mondingsenergie van 10,64 megajoule (10,64 miljoen joule). Dat is waarschijnlijk vergelijkbaar met de hoeveelheid energie in een auto van gemiddelde grootte die met 250 mph rijdt.

Ter vergelijking: het AK-47 geweer heeft een mondingssnelheid van 715 m / s (~ 1600 mph of ~ 2x de geluidssnelheid), met een mondingsenergie van ~ 2010 joules (ervan uitgaande dat 7,62x39 mm patronen worden gebruikt, maar dit kan variëren afhankelijk van het type munitie).

Hoewel het statistisch gezien niet erg indrukwekkend is als het gaat om railguns, aangezien echte railguns in staat zijn om snelheden te bereiken van mogelijk meer dan ~ 5000 m / s. Houd er rekening mee dat Mikoto een middelbare scholier is die acht schoten hiervan per minuut kan afvuren, wat vergelijkbaar is met "typische" railguns.

Ervan uitgaande dat de munt vergelijkbaar is met de grootte en het gewicht van een kwart van de VS, kan men aannemen dat de munt die ze gebruikt een gewicht heeft van ongeveer vijf gram. Met behulp van deze formule kunnen we de mondingsenergie krijgen:

Energie = 0,5 * (massa) (snelheid)² = 0,5 * (0,005 kg) (1030 m / s)² = ~ 2652,25 joule

Mikoto brengt dus wat meer schade aan dan een semi-automatisch aanvalsgeweer.

Maar dat is niet wat we nu zien, toch?

Niet helemaal. Maar wat kan zo'n verschil in output veroorzaken?

Volgens pagina 1, hoofdstuk 4 van de Railgun-manga, manipuleert ze elektromagnetisme om haar resultaten te bereiken. Dit lijkt aannemelijk, want als het magnetische veld voldoende gefocust was, zou ze theoretisch alleen de munt en / of objecten in de buurt kunnen versnellen.

Laten we nu de zwembadtest opnieuw bekijken, vanaf de zwembadreinigingsepisode (S1, aflevering 2) hebben we een geschatte schatting van de afmetingen van het zwembad:

Laten we dingen meten in termen van Kuroko's lengte (~ 152 cm)!

Aangezien het zwembad niet taps toeloopt of eindigt, gaan we ervan uit dat het zwembad ongeveer 14 Kurokos lang of ~ 21,28 m is (ja, het lijkt een beetje klein), en ongeveer 11 Kurokos breed, of ~ 16,72 m, bij de lijnen op de zwembadbodem en iets minder dan ~ 0.9 Kuroko, of laten we zeggen 1.36m diep.

Wat betreft het verplaatste water, wij kon probeer het volume van de waterpluim te integreren, ervan uitgaande dat het half en half lucht is, zoek het gewicht, enz. Maar we zullen hier lui zijn en aannemen dat 1 / 1000ste van het watervolume van het zwembad in de lucht werd verspreid toen Mikoto vuurt haar railgun. Het zwembad zou een volume hebben:

Inhoud = (1,36 m) * (21,28 m) * (16,72 m) = ~ 486,73 m³ van water

Aangezien het "zwaartepunt" de waterpluim vergelijkbaar lijkt te zijn in de buurt van de bovenkant van het gymnasium-achtige gebouw, gaan we een oogschatting maken van de deur in vergelijking met het gebouw, laten we aannemen dat het 10 m hoog is. Om de energie te berekenen die nodig is om zoiets te bereiken, doen we:

(Energie die nodig is om een object op te tillen) = (massa van het object) * (versnelling door zwaartekracht) * (hefhoogte).

Laten we in dit scenario een aantal hoeken afsnijden en aannemen dat alle energie van de opname wordt gebruikt om het water op te tillen (waarbij we de energie negeren die wordt besteed aan het opwarmen van het water, het creëren van de geluiden, luide explosies, elk dramatisch windeneffect), dan gaan we hebben

Energie = (1/1000) * (~ 486,73 m³) * (1000 kg / m³ water) * (9,8 m / s²) * (10m) = ~ 47699,54 joule

Als we het achterstevoren in de kinetische energievergelijking stoppen:

√ [(~ 47699,54 J) * 2 / (0,005 kg)] = ~ 4368,04 m / s

Dus de mondingssnelheid van haar railgun zou ~ 4368,04 m / s zijn.

We kunnen alleen maar aannemen dat, aangezien we de canonwaarde van 1030 m / s moeten respecteren, dat de schade veroorzaakt door het vermogen van Mikoto misschien te wijten is aan haar manipulatie van elektromagnetische straling die wordt veroorzaakt wanneer de munt door de lucht beweegt of een andere factor ... Maar maar nogmaals, wat weten we over de fysica van deze wereld waar wetenschap en magie naast elkaar bestaan?

@Krazer zo te zien, lijkt een semi-olympisch zwembad, 25m x 12.5m x 1.36m

+100

Elektriciteit kan het water verplaatsen:

De wiki zegt dat Misaka 1 miljard volt kan genereren.
(hoewel sommige bronnen 5 miljard volt aangeven, laten we bescheiden zijn )

Als ze de munt oplaadt, zou de snelle overdracht van lading van de munt naar het water afstoting veroorzaken tussen de munt en het omringende water, waardoor het water uit het zwembad wordt weggestuwd. De schokgolven zouden reflecteren op de randen en de bodem van het zwembad en het oppervlaktewater omhoog duwen.

Je kunt in de anime zien dat alle ontploffingen een zijwaartse beweging hebben, maar de TWEEDE ontploffing die wordt weergegeven, heeft een heel onderscheidend vermogen. zijwaartse beweging, wat erop duidt dat de impact het water ook een beetje naar de zijkanten duwt, aangezien het elektrisch geladen water van de munt weg beweegt terwijl de munt door het zwembad gaat.

De kwestie van de dissiperende lading is geen probleem. Ze kan bliksem richten, dus we kunnen aannemen dat haar elektromagnetische krachten ook de doorslagspanning van de lucht rond de munt kunnen veranderen (door de druk rond de munt te verhogen of door vacuüm te maken.

We moeten kijken naar de capaciteit van de munt

De straal van een kwart is 13 mm

Met een potentiaal van 1 miljard volt is de lading van de munt

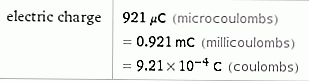
Nu kunnen we de elektrische kracht tussen de geladen munt en het geladen water berekenen, en laten we kortheidshalve aannemen:

de helft van de lading is overgebracht naar het water.
de muren en bodem van het zwembad zijn totaal isolant en onverwoestbaar.
de munt heeft de bodem geraakt zodra de helft van de lading is overgedragen.
Het water is 1 mm verwijderd van de munt

In deze situatie wordt de kracht tussen munt en water berekend met de wet van coulomb:

We komen hier bij de Megajoule.

Gegeven de massa van 10% van het water van het zwembad, geeft die kracht het water een tijdelijke versnelling van:

Om het water 100 meter op te tillen, moeten we het water met een snelheid van 44,3 m / s bedrukken

Dus de interactietijd tussen munt en water voordat de resterende energie verdwijnt, waardoor:

Krazer zei:
energie besteed aan het opwarmen van het water, het creëren van de luide explosie van geluiden, elk dramatisch windendeffect

En dat is

dat verklaart

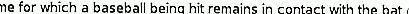
Zelfs als je rekening zou houden met de ladingsdissipatie, de afnemende afstotingskracht tussen het water en andere kleine aannames hier, is er genoeg energie voor alles.

Er is overal genoeg energie om te gebruiken zoals jij dat wilt.

Maar ik denk dat dit duidelijk verklaart waar de energie vandaan komt om het water op te tillen.

Ook als je de gebeurtenissen van latere afleveringen neemt, wanneer ze andere items dan een munt gebruikt

Een gigantische robotklauw en later een hele gigantische robot

je kunt zien dat de hoeveelheid opgeslagen energie groter is, en dat geldt ook voor de vernietigende kracht. Logisch, want de capaciteit van die items is groter dan die van een munt.

Veel dank aan Wolfram Alpha voor de berekeningen en afbeeldingen.

Meer theorieën:

Elektriciteit kan de munt blijven versnellen, zelfs nadat deze de "snuit" heeft verlaten.

Als ze de munt oplaadt, kan ze een nieuwe lading van hetzelfde teken op zichzelf genereren nadat de munt de "muilkorf" heeft verlaten. Dus zelfs als de munt met een snelheid van 1030 m / s vertrekt, zou ze hem kunnen versnellen, zelfs nadat hij was afgevuurd. Maar het is niet eens nodig, want ...

De spin van de munt en een van de meest destructieve krachten: Harmonics.

Zoals we kunnen zien in deze wikipedia-grafiek, neemt de energieoverdracht dramatisch toe zodra de maximale resonantie (1: 1) is bereikt. Windharmonischen zijn voldoende om een brug te vernietigen door deze te verplaatsen als een vioolsnaar. Als ze de munt kan draaien zodat de frequentie perfect overeenkomt met de harmonische frequentie van het zwembad, kan er enorme energie worden overgedragen.

Ik merkte net dat het water 9 seconden nodig zou hebben om 100 meter omhoog te gaan met 44,3 m / s. Omdat de explosie maar een paar frames duurt, kunnen we aannemen dat de contacttijd iets LANGER DAN 5 ms is en dat het opwaartse water verdunt / verdampt na het raken van 100 meter
Welnu, het zwembad is maar één voorbeeld, we zien haar vaak stoppen en auto's de lucht in blazen, genoeg warmte produceren om twee opeenvolgende metalen staven te smelten en een diepe kras achterlaten op de aarde waarover het reisde, zelfs zonder direct contact. Het lijkt alsof er naast de enorme snelheid van de munt nog een andere energie is.
Om nog maar te zwijgen over het feit dat ze in de Railgun-serie heeft laten zien dat ze andere voorwerpen dan een munt (namelijk een gigantische robotarm en een hele satelliet) met vergelijkbare snelheden kan voortstuwen.

Hoewel subjectief, was het vanaf het begin mijn sterke indruk dat de projectielcomponent indirect (en mogelijk niet relevant) is voor haar vermogen.

Ze kan produceren veel van energie
De energie gaat waar het projectiel gaat
Het is echter niet vastgesteld dat het projectiel draagt de energie

Het projectiel kan slechts een baken of focustype component zijn, mogelijk puur psychologisch (waarbij de techniek het tegenovergestelde is van het willekeurig afschieten van uitbarstingen van ongecontroleerde elektriciteit).

Ik herinner me dat ze in latere afleveringen een groot projectiel schoot, maar de bovenstaande speculatie kan nog steeds van toepassing zijn.

+1, dit is een geweldige uitleg IMO. Er is misschien een scène geweest waarin mensen een munt van haar vonden, maar ik herinner me dat veel vuren van haar railgun als de munt een balk was geworden, ik neem aan dat het tijdens het proces smelt (als er überhaupt iets van overblijft).
1 Een manier om dit te verifiëren, is om te zien of ze ooit iets niet-metalen als projectiel gebruikt. Als haar Railgun eigenlijk een Railgun is in wetenschappelijke zin, zou het moeten werken op iets dat kan worden versneld met elektromagnetisme, dus een soort metaal. Als ze niet-metalen voorwerpen kan gebruiken, dan is het eigenlijk geen railgun en deze uitleg zou erg overtuigend zijn.

Ik beargumenteer dat het een geval van Anime Physics is door de alternatieve mogelijkheden te weerleggen die je hebt voorgesteld.

Je hebt gelijk - het dragen van zoveel energie als traagheidsmoment is onmogelijk. Zelfs de superkrachten van Misaka zijn een wereld verwijderd van relativistische snelheden.
De energie kan niet als lading in de munt worden opgeslagen, omdat deze als "bliksem" zou verdwijnen.
De energie kan niet afkomstig zijn van massa-energie. Naast de resulterende dodelijke straling, zou het vrijgeven van massa-energie zonder antimaterie betekenen dat er kernenergie vrijkomt. Kernenergie kan alleen onder extreme druk vrijkomen (kernreacties in bommen worden geïnitieerd door uranium samen te persen met de ontploffing van een kleinere bom). Als iemand een voorbeeld zou kunnen vinden van Misaka die haar munt vond nadat ze erop had geschoten, zal dat duidelijk het argument van massa-energie weerleggen.

Ten slotte hebben de Mythbusters in deze video bewezen dat een munt die driemaal zo snel reist als het geluid (rond de snelheid van een kogel) slechts beton deukt.

Het is ook vermeldenswaard dat (voor zover ik me goed herinner) de 'paranormale' krachten van het type Misaka losjes gebaseerd zijn op de immer populaire, fantastische, dubbele verkeerde interpretatie van het gedachte-experiment van Schr dinger: die perceptie beïnvloedt realiteit, en dus de perceptie op de juiste manier veranderen, zou de realiteit moeten veranderen. (Of zoiets. Er klonk techno-gebabbel in de omgeving, maar dat leek de kern ervan te zijn.)

Dus een alternatieve, hoewel minder interessante verklaring van de onevenredige effecten van haar railgun zou iets zijn in de trant van: Misaka's eigen perceptie van hoe krachtig het railgun zou moeten zijn, is verkeerd, resulterend in overdreven effecten.

Jullie vergeten allemaal het fundamentele feit dat de meting van 1030 m / s werd uitgevoerd terwijl ze in water schoten. De effecten van weerstand op de munt die in water wordt afgevuurd, zijn veel groter in omvang dan de effecten van weerstand terwijl deze door de lucht wordt afgeschoten. Lucht is bijna duizend keer minder dicht dan water. Als we de vergelijking voor weerstand uitvoeren, komen we uit op een krachtmagnitude op de munt van 18.466 Newton. [18466 = 0,5 * 1000 kg / m ^ 3 * (1030 m / s) ^ 2 * 0,82 * 0,000042455 m ^ 2]

.82 is de weerstandscoëfficiënt voor een lange cilinder zoals een arcademunt, 1000kg / m ^ 3 is de dichtheid van water en .000042455m ^ 2 is de dwarsdoorsnede van de afgevuurde munt.

als we de vergelijking in omgekeerde volgorde uitvoeren om de snelheid van de munt in de lucht te achterhalen, houden we een snelheid van 29.428 m / s over.

Klinkt veel meer als een echt railkanon, nietwaar?

'A Certain Magical Index' heeft 50 oneven lichte romans, 13 delen manga, 2 seizoenen anime, een film en een paar videogames.

'A Certain Scientific Railgun' heeft 2 lichte romans, 11 volumes manga, 2 seizoenen anime, een OVA en een eigen videogame.

In geen van deze bronnen (die ik me in ieder geval kan herinneren) wordt de truc van Misaka geïmpliceerd dat het iets anders is dan een arcade-token (geen munt, daarom is het zelfs ijzerhoudend om mee te beginnen) dat drie keer zo snel is als het geluid.

En er is nog een andere rare eigenschap van de railgun-aanval: Touma, de jongen met de anti-magische vuist, kan hem vangen. (Zoals te zien in hoofdstuk 7, deel 1 van de Railgun-manga.)

Aangezien Touma het kan verdrijven, betekent dit dat er nog steeds iets bovennatuurlijks aan de munt is, zelfs als deze smelt. Die bovennatuurlijke eigenschap zal de reden zijn waarom het een duwkracht heeft die ver boven wat het zou moeten hebben op momentum alleen.

Ik heb geen bewijs voor mijn volgende punt, maar ik geloof dat het magnetische veld van Misaka gewoon doorgaat met het indrukken van de munt, ver nadat hij haar hand heeft verlaten. Dat zou beide eigenaardigheden mooi verklaren.

Laten we in de aflevering niet vergeten dat ze de robotarm deed die ze deed omdat de persoon buiten het bereik van haar munten zat. Aan het einde van de balk was er gewoon geen munt meer. Ze legde uit terwijl ze die arm blokkeerde, ving en afvuurde dat er een reden is waarom ze gewoonlijk munten gebruikt.

Ik vermoed dat verschillende factoren samen bijdragen aan haar destructieve potentieel, waaronder haar aangewezen badass-status, aanhoudende versnelling, traagheid, spin, hypersonische schokgolf en mogelijke omzetting van materie in plasma.

Onthoud dat ze waarschijnlijk ook energie afleidt om terugslag en andere destructieve aspecten van het afvuren van het railgun te bestrijden. Die afscherming is voldoende om gerichte meervoudige nucleaire ontploffingen te stoppen die in staat zijn om snel door beton en staal te smelten, ondanks dat Misaka op dat moment uitgeput was. Ik weet zeker dat dit voldoende energie kan zijn om een secundaire versnelling te veroorzaken.

Het is een geval van anime-fysica waar andere posters op hebben gezinspeeld, maar niet je gemiddelde anime-fysica, er wordt in bepaalde delen van de manga en de zusterserie-index gezegd dat de manier waarop esper-krachten werken, is door een realiteitsvervormingsveld te manipuleren om in de stijl van hun krachten. daarom werkt het railgun van misaka omdat het voldoende energie en wiskunde van de werkelijkheid heeft